Monte Carlo 蒙特卡洛模拟，简称 MC.

Markov Chain Monte Carlo 是用马尔科夫链采样的蒙特卡洛模拟，简称 MCMC.

Monte Carlo 模拟

这个比较简单了，举个例子，要计算 π 的近似值，可以在一块正方形板子里画一个内接圆，然后以均匀的概率往正方形里一粒一粒地扔沙子，每扔一粒，就判断并且记录这里沙子在圆内还是圆外，然后把沙子吹掉，如此往复。圆的面积是 πr²，正方形的面积是 4r²，所以落在圆内的概率（圆内沙子的数量和总数的比值）乘 4，就是所求。

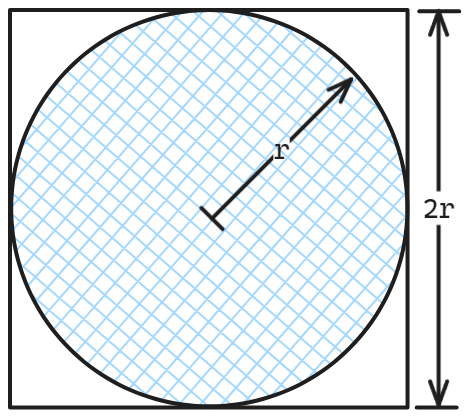
归纳一下：当问题的解用一个随机变量的概率分布、期望值、二阶矩……等等来表示的时候，就生成一个符合该概率分布的随机样本，用样本的统计量去近似原概率分布。

Markov Chain Monte Carlo

但是前述例子有一个步骤，就是我们往板子上扔完沙子要把沙子吹掉，每粒沙子，每次扔沙子之间也应该看不出区别，这是为了保证取样之间相互独立且来自同一个概率分布。

但是很多取样过程无法满足这种条件，或者达成条件所需的成本很高。比如计算一个高斯积分 \(\int_{-\infty}^{+\infty}e^{-x^2}dx\)，被积函数的取值范围涵盖整个实数集，想找一个在整个实数集上均匀分布的随机数发生器就比较难了。

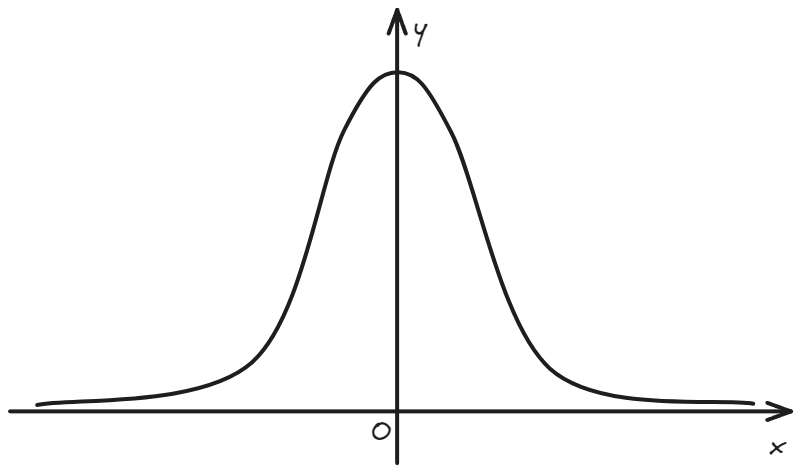
但是学过物理的朋友应该知道，上面的被积函数是以狄拉克 δ(x) 函数为初值条件的一个扩散方程的解，在某一时刻的空间分布。（不想凑系数了，将就看吧）

而扩散方程又是随机游走 (random walk) 在连续近似下的极限。

所以我们直接模拟一堆粒子从原点出发作随机行走，向两个方向的概率相同，扩散系数以及积分里的常数对齐，统计粒子在整个过程中出现在不同 x 位置的频率，求和之后乘以步长就是积分结果。这个过程需要的随机数发生器容易获取得多，是一个以 0.5 为阈值的 [0,1) 的均匀分布，比如一个均匀硬币。

而随机行走过程中走完每一步的位置，都只取决于前一步的位置，而与更久远的历史无关——这样的过程叫做马尔可夫过程。用这种方法取样获得随机样本的蒙特卡洛模拟，就是 MCMC.

扩散方程和随机行走只是 MCMC 的一个很特殊很特殊的例子，而对于一般的 MCMC 模拟，有以下通用的 Markov Chain 采样的算法：

Metropolis-Hastings 算法

已知一个随机变量 x, 和一个与目标概率分布 P(x) 成正比的函数 f(x)（不要求 f 归一化）

1. 初始化
   1. 选定初始采样点 \(x_0\)
   2. 选定一个采样函数 proposal function，也就是在已知当前 x 的取值时，下一个 x’ 取值的概率分布 \(g(x’\vert x)\)；其中对于 Metropolis 算法，这个采样函数是对称的：\(g(x’\vert x)=g(x\vert x’)\). 常用以两者之差为宗量的高斯函数。
2. 在得出 t 时刻的 \(x_t\) 之后：
   1. 根据 \(g(x'\vert x_t)\) 抽样得到一个 x’
   2. 计算 α = f(x’)/f(x) = P(x’)/P(x)
   3. 决定是否将 x’ 加入样本
      1. 如果 α ≥ 1, 直接加入
      2. 如果 α < 1, 以 α 为概率加入

这种方法不保证采样的早期样本也符合目标概率分布，所以一般会抛弃最先加入的若干样本。

Gibbs 采样

只是一种思路，不算是完整的算法。

当被采样的随机变量是一个多维向量的情况，在不使用 Gibbs 采样的情况下，在迭代的某一步骤 t，每个分量都应该是前一步骤的函数：\(x_{i,t}=f(\{x_{j,\ t-1}\})\)

而 Gibbs 采样就是说，不必让每个维度 i 都根据前一个步骤的分量来取值，可以把当前 t 已经取样出来的分量直接带入到本回合后面的维度：\(x_{i,t}=f(\{x_{j,\ t}\}_{j<i}\cup\{x_{k,\ t-1}\}_{k\ge i})\)