这些内容总结自美国研究生级别的《数学物理方法》两次课的笔记,大约两个小时。
如果是中国大学本科的话,认真的老师半个小时庶几可以讲完;
念 PPT 就算上课的话 15 分钟可以讲完,附赠一个段子;
翻转课堂的话也就布置个作业,老师一句话可以讲完。
以上数据除第一句外纯属揣测,没有黑任何人的意思,love and peace~
扩散方程
带有初值条件的扩散方程表述如下:
\[\begin{cases} u(x,t=0)=f(x) \\ \partial u(x,t)/\partial t=\sigma \cdot \partial^2 u(x,t)/ \partial x^2 \end{cases}\]方程的解为:
\[u(x,t) = \frac{1}{\sqrt{4\pi \sigma t}} \int_{-\infty}^{+\infty} f(s)\ e^{-\frac{(x-s)^2}{4\sigma t}}\ ds\]解法是将 u(x,t) 对空间变量 x 作傅里叶变换为 U(k,t),利用傅里叶变换的性质,变换后的方程将是关于时间 t 的一阶常微分方程。求解后作傅里叶逆变换 即为上式。 (完蛋,好久没做题了,那个 \(e^{-\frac{(x-s)^2}{4\sigma t}}\) 是怎么凑出来的,为什么我直接给消掉了啊) 凑出来了凑出来了,初值条件代入频域 k 空间里的通解来确定积分常数,可以看到结果 \(F(k) e^{-\sigma t k^2}\) 是两项之积,所以根据傅里叶变换的卷积定理,实空间 x 里的解是 f(x) 和 \(\mathscr{F}_{k\rightarrow x}^{-1}\{e^{-\sigma t k^2}\}\) 的卷积(所以上式的指数项以 (x-s) 为宗量),而计算后者的时候需要用到高斯积分~
随机游走
随机游走是一个离散过程,为了和连续时空中的扩散方程相对比,将空间变量 x 离散化为相隔 Δ 的格点 i,时间变量 t 离散化为相隔 δ 的 n。
当一个粒子在 n 时刻位于格点 i 时,在下一个时刻 n+1, 它有 1/2 的概率移动到 i-1, 1/2 的概率移动到 i+1.
所以,虽然每个进行随机游走的粒子在任意时刻都只有确定且唯一的位置,但是对于大量同样初始位置和运动规律的例子,n 时刻出现在 i 格点的概率 P(i,n) 有以下关系:
\[\begin{cases} P(i,0)= f_i \\ P(i,n)=\frac{1}{2}\left[P(i-1,n-1)+P(i+1,n-1)\right] \end{cases}\]在初值条件为 \(f_i=\delta_{i=0}\) 时,递推结果如下:
| x 轴 — | i = -4 | i = -3 | i = -2 | i = -1 | O | i = 1 | i = 2 | i = 3 | i = 4 | → |
|---|---|---|---|---|---|---|---|---|---|---|
| n = 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| n = 1 | 0 | 0 | 0 | 1/2 | 0 | 1/2 | 0 | 0 | 0 | |
| n = 2 | 0 | 0 | 1/4 | 0 | 1/2 | 0 | 1/4 | 0 | 0 | |
| n = 3 | 0 | 1/8 | 0 | 3/8 | 0 | 3/8 | 0 | 1/8 | 0 | |
| t 轴 ↓ |
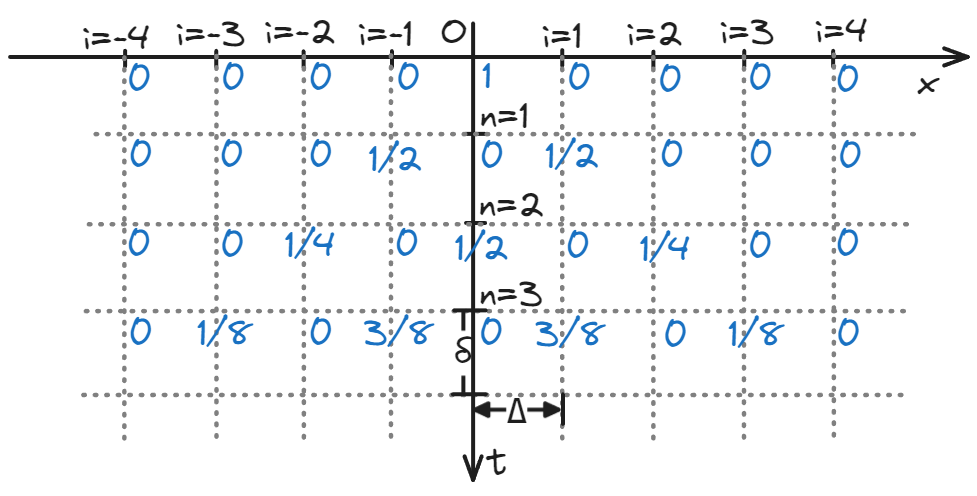
离散的情况,很难对任意的初值条件写出解的表达式,但是对于上面的特殊情况,课上不加证明地给出了(可能是根据上图凑出来的)下面的解:
\[P(i,n)=\frac{1}{2^n}\frac{n!}{\left(\frac{n+i}{2}\right)!\left(\frac{n-i}{2}\right)!}\]对的,以上关系只能表示 (n+i = 偶数) 的情况,但是康托尔告诉了我们,所有偶数和所有自然数的“数量”一样多,所以也没差太多~
方程的等价
概率的递推公式可以变换为:
\[\frac{1}{\delta}\left[P(i,n)-P(i,n-1)\right]=\frac{1}{2}\left [\frac{P(i-1,n-1)-2P(i,n-1)+P(i+1,n-1)}{\Delta^2}\right]\frac{\Delta^2}{\delta}\]因为 \(x=i\Delta,\ t=n\delta\), 对两个变量的微分可以离散化成差分:
\[\frac{\partial}{\partial x}\rightarrow \frac{1}{\Delta}\left[()_i-()_{i-1}\right],\ \frac{\partial}{\partial t}\rightarrow \frac{1}{\delta}\left[()_n-()_{n-1}\right]\]直接就能看出扩散方程和随机游走的等价,且系数之间存在关系:\(\sigma = \frac{\Delta^2}{2\delta}\)
解的等价
只讨论一个 δ(x) 函数作为初值条件的情况,我们要证明此时扩散方程的解:
\[u(x,t) = \frac{1}{\sqrt{4\pi \sigma t}} e^{-\frac{x^2}{4\sigma t}}\ \xleftarrow[{\Delta,\delta \rightarrow 0;\ i,n\rightarrow \infty}]{x=i\Delta,\ t=n\delta} \frac{1}{2^n}\frac{n!}{\left(\frac{n+i}{2}\right)!\left(\frac{n-i}{2}\right)!} \frac{1}{2\Delta}\]只需讨论这一个情况,因为 δ(x-s) 函数可以看作将一个函数 f(x) 在自变量 x=s 时切片为 f(s),而任何一个(性质比较“优美”的)函数都可以看作把它自己在定义域上的所有点切片后再重新叠加起来:
\[f(x) = \int_{-\infty}^{+\infty}f(s)\delta(x-s)\ ds\]过程需要用到 Sterling 公式对阶乘的近似:\(n! \approx \sqrt{2\pi n}\ n^n e^{-n}\)
\[\begin{array}{rcl} \frac{P(i,n)}{2\Delta} & \approx & \frac{1}{2\Delta} \frac{1}{2^n} \frac{\sqrt{2\pi n}\ n^n e^{-n}}{\sqrt{\frac{2\pi (n-i)}{2}}\ \left(\frac{n-i}{2}\right)^{\frac{n+i}{2}} e^{-\frac{n+i}{2}}\sqrt{\frac{2\pi (n+i)}{2}}\ \left(\frac{n+i}{2}\right)^{\frac{n+i}{2}} e^{-\frac{n+i}{2}}} \\ & = & \frac{1}{2\Delta}\frac{\sqrt{2n}}{\sqrt{\pi(n^2-i^2)}}\frac{n^n}{(n-i)^{\frac{n}{2}-\frac{i}{2}}(n+i)^{\frac{n}{2}+\frac{i}{2}}} \\ & = & \frac{1}{2\Delta}\frac{\sqrt{2n}}{\sqrt{\pi(n^2-i^2)}}\frac{n^n/n^n}{(n-i)^{\frac{n}{2}}(n+i)^{\frac{n}{2}}(n-i)^{-\frac{i}{2}}(n+i)^{\frac{i}{2}}/n^n} \\ & = & \frac{1}{2\Delta}\frac{\sqrt{2n}}{\sqrt{\pi(n^2-i^2)}} \frac{1}{\left(1-\frac{i}{n}\right)^\frac{n}{2}\left(1+\frac{i}{n}\right)^\frac{n}{2}\left(1-\frac{i}{n}\right)^{-\frac{i}{2}}\left(1+\frac{i}{n}\right)^\frac{i}{2}} \\ & = & \frac{1}{\sqrt{2}\Delta}\frac{1}{\sqrt{\pi(n-\frac{i^2}{n})}} \frac{1}{\left(1-\frac{i^2}{n^2}\right)^\frac{n}{2}\left(1-\frac{i}{n}\right)^{-\frac{i}{2}}\left(1+\frac{i}{n}\right)^\frac{i}{2}} \\ & \xrightarrow[\frac{i}{n}=\frac{x\Delta}{2\sigma t},\ \frac{i^2}{n}=\frac{x^2\delta}{\Delta^2 t}]{(1+a\epsilon)^{1/\epsilon}\rightarrow e^a} & \frac{1}{\sqrt{4\pi\sigma t}}\frac{1}{e^\frac{x^2}{4\sigma t} e^\frac{x^2}{4\sigma t} e^{-\frac{x^2}{4\sigma t}} } \\ & = & \frac{1}{\sqrt{4\pi\sigma t}}e^{-\frac{x^2}{4\sigma t}} \end{array}\]之前 MCMC 讲错了
讲 Markov Chain Monte Carlo 模拟的时候举的例子是计算 \(\int_{-\infty}^{+\infty}e^{-x^2}dx\), 现在系数可以对上了:\(1=4\sigma t=4 \frac{\Delta^2}{2\delta} n\delta = 2\Delta^2n\), 随机游走的步数和步长之间存在一个确定的关系,在步长确定的情况下,我们需要重复模拟大量粒子作相同步数的随机游走,然后统计这一确定步数走完之后的每个粒子的终末位置。
所以,这并不是一个 Markov Chain Monte Carlo 模拟,只是一个普通的 Monte Carlo 模拟,我们拿到了想要知道的随机变量的原始概率分布,只不过取得这一概率分布的过程是一个 Markov 过程。
正经的 MCMC,应该是只模拟一个粒子作随机行走,然后把它每一步的位置记录下来,统计到样本里去。这样的话时间 t 的信息就被抹去了,而且由于扩散方程描述的状态并不是热力学平衡态,并不能通过统计物理中的遍历性 (ergodicity) 来得到正确结果。
采用了 Metropolis 算法的 MCMC, 一个粒子作随机行走只是其中的一个步骤,还要计算这一步之前和之后 \(e^{-x^2}\) 的值,来决定这一步是否被加入样本,不成立的话要退回前一步继续走。